В математиката сумирането (означено с големия гръцки символ сигма) е набор от сумирани числа. Каква е сумата? Това е резултат от подобно действие. Ако числата се добавят едно след друго отляво надясно, тогава междинният резултат е частична сума.
Каква е сумата?
Числата, които трябва да се сумират, могат да бъдат цели, рационални, реални или комплексни. В допълнение към тях могат да се добавят други типове стойности: вектори, матрици, полиноми и изобщо елементи от всяка адитивна група (или дори моноид).
Ако броят на елементите на термините е краен, тогава сумирането винаги дава добре дефинирана стойност. Сумирането на безкрайна последователност от стойности се нарича серия. Неговата стойност често може да бъде определена с помощта на ограничение (въпреки че понякога стойността може да бъде безкрайна).
Поредици
Сборът на числата [3, 7, 2, 1] може да бъде дефиниран чрез израз, чиято стойност е сумата от цифрите, включени в него, например 3 + 7 + 2 + 1=13. Тъй като допълнениеасоциативно, сумата не зависи от това как са групирани термините, например (3 + 7) + (2 + 1) и 3 + ((7 + 2) + 1) и двете са равни на девет, така че скоби обикновено са освободено от. Събирането също е комутативно, така че пренареждането на членовете не променя стойността на сумата. Имайте предвид, че това свойство може да не работи за безкрайно сумиране.

Няма специална нотация за сумиране на последователности от този вид. Има само лек нюанс, ако има по-малко от два елемента. Сумирането на последователност от един член не съдържа знак плюс (не се различава от формата на самото число) и ако изобщо няма елементи, тогава дори не може да бъде написано (но вместо това може да се обозначи с неговата стойност "0"). Ако обаче термините на последователността са определени от специфичен модел, като функция, тогава операторът за сумиране може да бъде полезен или дори съществен.
Запис
За да разберете какво представлява сумата, е необходимо също да анализирате външния й вид.
За сумиране на поредица от цели числа от 1 до 100 често се използва израз, който включва многоточие за обозначаване на липсващите членове: 1 + 2 + 3 + 4 + … + 99 + 100. Моделът е доста лесно да се види в този пример. Въпреки това, за по-сложни опции е необходимо да се посочи точно правилото, използвано за намиране на стойността на елементите, което може да се постигне с помощта на оператора за сумиране "Σ". Използвайки този символ (сигма), можете да приложите следната нотация:
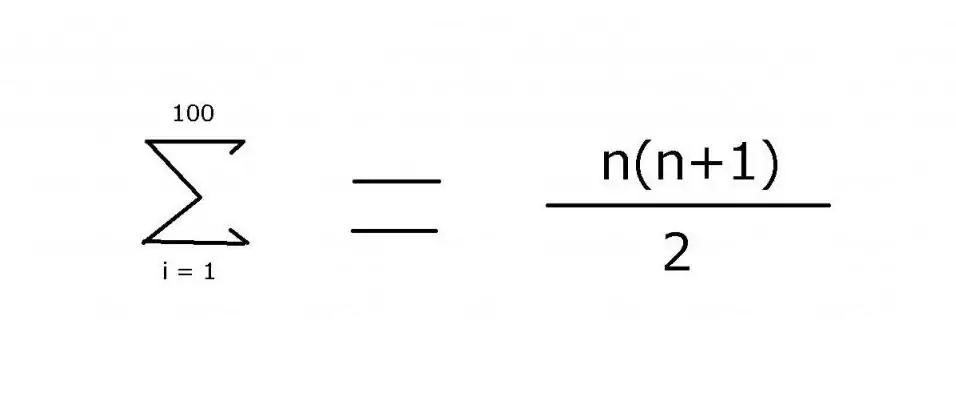
Стойността на този израз е 5050. Може да се намери с помощта на математическа индукция, откъдето идва втората част на формулата.
За различни последователности формулата ще се промени. Процесът на запис се свежда до търсене на предобраз на някаква безкрайна последователност и след това описването му с формула. След като направите това, не е трудно да разберете каква е сумата в конкретен случай.
Когато е необходимо да се изясни, че числата се събират заедно с техните знаци (плюс или минус), се използва терминът алгебрична сума. Например, в теорията на електрическите вериги законите на Кирхоф разглеждат алгебричния сбор от токове в мрежа от проводници, срещащи се в точка, давайки противоположни знаци на токовете, вливащи се и излизащи от възел.






