Естествените геометрични шарки или шарки се появяват като повтарящи се форми, които понякога могат да бъдат описани или представени от математически модели.
Геометрията в природата и живота идва в много форми и форми, като симетрия, спирали или вълни.
История
За първи път древногръцките философи и учени - Питагор, Емпедокъл и Платон - се заеха с въпросите на геометрията в природата. Чрез анализиране на примери за предвидими или идеални геометрични форми в растенията и животните, те се опитаха да демонстрират ред и симетрия в природата.
Съвременните опити за изучаване на геометрията в природата започват през 19-ти век с усилията на белгийския физик Джоузеф Плато, който разработва концепцията за минималната повърхност на сапунен мехур. Първите съвременни опити първо се концентрират върху демонстрирането на идеални и предвидими геометрични форми, а след това се насочват към разработването на модели, които предсказват появата и проявата на геометрията в природата.
През 20-ти век математикът Алън Тюринг работи върху механизмите на морфогенезата, което обяснява появата при животнитеразлични шарки, ивици, петна. Малко по-късно биологът Аристид Линденмайер, заедно с математика Беноа Манделброт, ще завършат работата по математическите фрактали, които повтарят моделите на растеж на някои растения, включително дървета.
Наука
Съвременните науки (математика, физика и химия), с помощта на технологии и модели, се опитват не само да обяснят, но и да предскажат геометричните модели, намиращи се в природата.
Формата и цветът на много живи организми, като паун, колибри и морски раковини, са не само красиви, но и геометрично правилни, което привлича любопитството на учените. Красотата, която наблюдаваме в природата, може да бъде причинена естествено, математически.
Наблюдаваните естествени модели в математиката се обясняват с теорията на хаоса, която работи със спирали и фрактали. Такива модели се подчиняват на законите на физиката, освен това физиката и химията, използвайки абстрактна математика, предсказват формите на кристалите, както естествени, така и изкуствени.
Биологията обяснява геометрията в природата чрез естествен подбор, където такива редовни характеристики като ивици, петна, ярки цветове могат да се обяснят с необходимостта от маскиране или изпращане на сигнали.
Видове модели
В природата има много повтарящи се модели, които се появяват в различни геометрични форми. Видове основни закономерности на геометрията в природата, снимки и техните описания можете да намерите по-долу.
Симетрия. Тази геометрична форма е една от най-често срещаните в природата. Най-често при животниогледална симетрия - пеперуди, бръмбари, тигри, сови. Среща се и в растения, като кленови листа или цветя на орхидея. В допълнение, симетричната геометрия в природата може да бъде радиална, петлъчева или шесткратна, като снежинки.

Фрактали. В математиката това са самоподобни конструкции, които са безкрайни. В природата е невъзможно да се открие такава безкрайна самоповтаряща се форма, следователно приближенията на фрактални модели в природата се наричат геометрични фрактали. Такава геометрия може да се наблюдава в природата в листа от папрат, броколи, плодове от ананас.
Спирали. Тези форми са особено разпространени сред мекотелите и охлювите. Учените наблюдават спирални форми в космоса, например спирални галактики. Спиралата се нарича златно съотношение на Фибоначи.

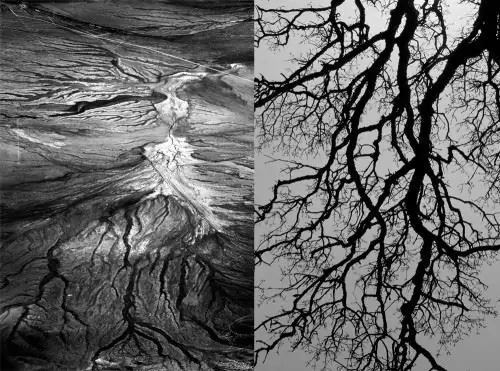
Меандри. Случайността на динамичните системи в математиката се проявява в природата под такива форми като меандри и потоци. Естествената геометрия приема формата на прекъсната или по-скоро извита линия, като речен поток.
Вълни. Те се причиняват от смущения и движения на въздуха, ветрови течения, разпространявани както във въздуха, така и във водата. В природата това са не само морски вълни, но и пустинни дюни, които могат да образуват геометрични форми - линии, полумесеци и параболи.
Мозайка. Създаден чрез повтаряне на едни и същи елементи на повърхността. Мозаечната геометрия в дивата природа се среща при пчелите: те строяткошер с пчелни пита - повтарящи се клетки.

Формиране на модели
В биологията образуването на геометричен цвят се дължи на процеса на естествен подбор. Още в средата на 20-ти век Алън Тюринг успява да опише механизма за появата на петна и ивици в цвета на животните - той го нарече реакционно-дифузионен модел. Някои клетки на тялото съдържат гени, които се контролират от химични реакции. Морфогенът води до образуване на кожни участъци с тъмен пигмент (петна и ивици). Ако морфогенът присъства във всички кожни клетки - получава се цветът на пантерата, ако присъства неравномерно - обичайния петнист леопард.






