Когато партньорска проверка, например, оценка на конкурентоспособността на продуктите, е необходимо, както във всяка научна работа, да се извърши статистическа обработка на данни. Последното започва с определяне на съгласуваността на експертните заключения, чието числово изразяване е коефициентът на съгласуване.
Защо се нуждаем от експертна консенсусна оценка?
Тази оценка е необходима преди всичко, тъй като мненията на експертите могат да се различават значително по оценените параметри. Първоначално оценката се извършва чрез класиране на показателите и приписването им на определен коефициент на значимост (тежест). Непоследователното класиране води до това, че тези коефициенти са статистически ненадеждни. Мненията на експерти с необходимия им брой (повече от 7-10) трябва да се разпределят съгласно нормалния закон.
Концепцията за коефициента на съгласуваност
И така. Последователността е съгласуваност. Коефициентът е безразмерна величина, показваща съотношението на дисперсията към максималната дисперсия в общия случай. Нека обобщим тези понятия.
Коефициентът на съгласуване е число от 0 до 1, показващо последователността на експертните мнения, когатокласиране на някои имоти. Колкото по-близо е тази стойност до 0, толкова по-ниска се счита консистенцията. Ако стойността на този коефициент е по-малка от 0,3, мненията на експертите се считат за непоследователни. Когато стойността на коефициента е в диапазона от 0,3 до 0,7, последователността се счита за средна. Стойност, по-голяма от 0,7, се счита за висока последователност.
Случаи на използване
При провеждане на статистически изследвания могат да възникнат ситуации, при които обект може да се характеризира не с две последователности, които се обработват статистически с помощта на коефициента на съгласуваност, а с няколко последователности, които съответно се класират от експерти със същото ниво на професионализъм в определена област.
Трябва да се определи последователността на класирането, извършено от експерти, за да се потвърди правилността на хипотезата, че експертите правят относително точни измервания, което позволява формирането на различни групировки в експертни групи, които до голяма степен се определят от човешки фактори, предимно като различия във възгледите, концепциите, различните научни школи, естеството на професионалната дейност и т.н.
Кратко описание на метода за класиране. Неговите предимства и недостатъци
При класиране се използва методът за класиране. Същността му се крие във факта, че на всяко свойство на обекта се присвоява собствен специфичен ранг. Освен това на всеки експерт, включен в експертната група, се присвоява този рангнезависимо, което води до необходимостта от обработка на тези данни, за да се установи съгласуваността на експертните мнения. Този процес се извършва чрез изчисляване на коефициента на съгласуваност.
Основното предимство на метода за ранг е неговата лекота на прилагане.
Основните недостатъци на метода са:
- малък брой обекти за класиране, тъй като когато броят им надвиши 15-20, става трудно да се присвоят обективни точки за класиране;
- Въз основа на използването на този метод остава отворен въпросът колко далеч са изследваните обекти един от друг по значение.
Когато се използва този метод, трябва да се има предвид, че оценките се основават на някакъв вид вероятностен модел, така че трябва да се прилагат с повишено внимание, като се има предвид обхвата.
Коефициент за ранг на съответствие на Кендъл
Използва се за определяне на връзката между количествени и качествени характеристики, характеризиращи хомогенни обекти и класирани по същия принцип.
Този коефициент се определя по формулата:
t=2S/(n(n-1)), където
S - сумата от разликите между броя на последователностите и броя на инверсии на втория елемент;
n - брой наблюдения.

Алгоритъм за изчисление:
- Стойностите x са подредени във възходящ или низходящ ред.
- Y-стойностите са подредени в реда, в който съответстват на x-стойностите.
- За всеки следващ ранг на y определете колко стойности на по-висок ранг го следват. Те се сумират и се изчислява мярката за съответствие на последователности от рангове по x и y.
- По същия начин се изчислява броят на ранговете на y с по-ниски стойности, които също се сумират.
- Добавете броя на ранговете с по-високи стойности и броя на ранговете с по-ниски стойности, което води до стойността S.
Този коефициент показва връзката между две променливи и в повечето случаи се нарича коефициент на корелация на ранг на Кендъл. Такава зависимост може да бъде представена графично.
Определяне на коефициент
Как се прави? Ако броят на класираните характеристики или фактори надвишава 2, се използва коефициентът на съгласуване, който по същество е множествен вариант на корелация на ранга.
Бъдете внимателни. Изчисляването на коефициента на съгласуваност се основава на съотношението на отклонението на сумата от квадратите на ранговете от средната сума на квадратите на ранговете, умножена по 12, към квадрата на експертите, умножена по разликата между куба на числото на обектите и броя на обектите.
Алгоритъм за изчисление
За да разберем откъде идва числото 12 в числителя на формулата за изчисление, нека разгледаме алгоритъма за определяне.
За всеки ред с ранговете на определен експерт се изчислява сумата от ранговете, която е произволна стойност.
Коефициентът на съгласуване обикновено се дефинира като съотношението на оценката на дисперсията (D) към максималната стойност на оценката на дисперсията(Dmax). Нека последователно формулираме дефинициите на тези количества.
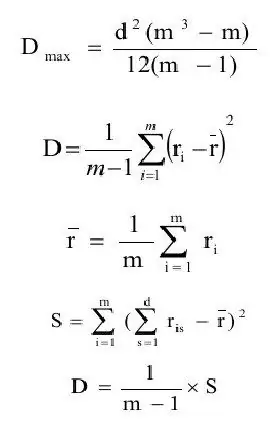
където rср. - оценка на очакванията;
m - брой обекти.
Замествайки получените формули по отношение на D към Dmax получаваме окончателната формула за коефициента на съгласуване:
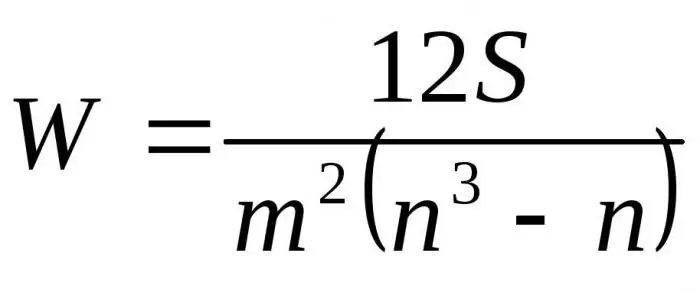
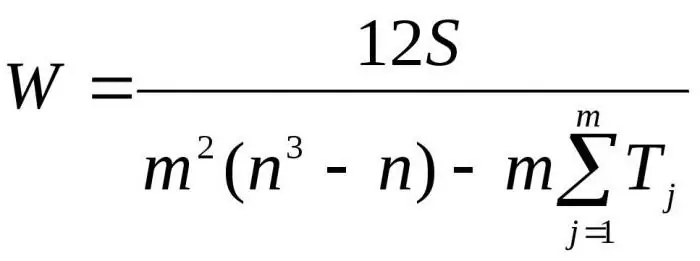
Тук m е броят на експертите, n е броят на обектите.
Първата формула се използва за определяне на коефициента на съответствие, ако няма свързани рангове. Втората формула се използва, ако има свързани рангове.
И така, изчисляването на коефициента на съгласуваност приключи. Какво следва? Получената стойност се оценява за значимост с помощта на коефициента на Пиърсън, като този коефициент се умножи по броя на експертите и по броя на степените на свобода (m-1). Полученият критерий се сравнява със стойността на таблицата и ако стойността на първата надвишава последната, те говорят за значимостта на изследвания коефициент.
В случай на свързани рангове, изчисляването на критерия на Пиърсън става малко по-сложно и се извършва чрез следното съотношение: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Пример
Да приемем, че експертният метод оценява конкурентоспособността на маслото, продавано в търговската мрежа. Нека дадем пример за изчисляване на коефициента на съгласуваност. Преди да се оцени конкурентоспособността, е необходимо да се класира потребителятсвойства на този продукт, които участват в оценката. Да приемем, че тези свойства ще бъдат следните: вкус и мирис, консистенция и външен вид, цвят, опаковка и етикетиране, съдържание на мазнини, търговско наименование, производител, цена.
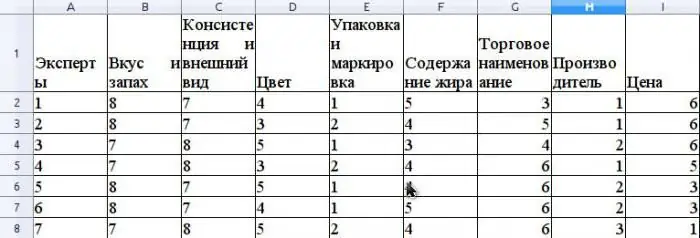
Да приемем, че експертната група се състои от 7 експерти. Фигурата показва резултатите от класирането на тези свойства.
Средната стойност на r се изчислява като средна аритметична и ще бъде 31,5. За да намерите S, сумирайте квадратните разлики между rе и r средно, съгласно формулата по-горе и определете, че стойността на S е 1718.
Изчислете коефициента на съгласуване, като използвате формулата, без да използвате свързани рангове (ранговете биха били свързани, ако един и същ експертен съветник имаше едни и същи рангове за различни свойства).
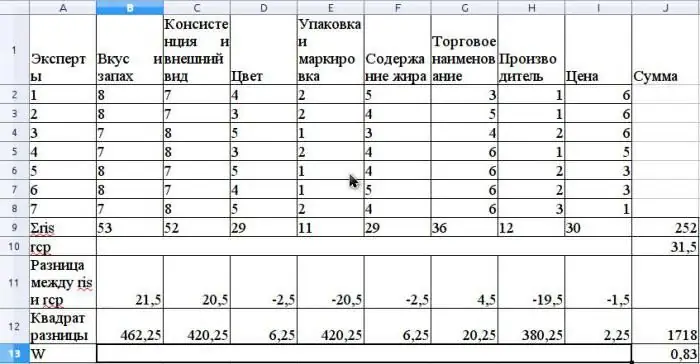
Стойността на този коефициент ще бъде 0,83. Това показва силен консенсус сред експертите.
Проверете значението му с помощта на теста на Пиърсън:
7 x 0,83 x (8-1)=40,7.
Табичният тест на Пиърсън при 1% ниво на значимост е 18,5, а при 5% - 14,1.
Примерът демонстрира простотата и достъпността на изчислението за всеки човек, който знае основите на математическите изчисления. За да ги облекчи,използвайте формуляри за електронни таблици.
В заключение
По този начин коефициентът на съгласуваност показва съгласуваността на мненията на няколко експерти. Колкото по-далеч е от 0 и по-близо до 1, толкова по-последователни са мненията. Тези коефициенти трябва да бъдат потвърдени чрез изчисляване на критерия на Пиърсън.






