Модулът на еластичност е физическа величина, която характеризира еластичното поведение на материала, когато към него се приложи външна сила в определена посока. Еластичното поведение на материала означава неговата деформация в еластичната област.
История на изследването на еластичността на материалите

Физическата теория на еластичните тела и тяхното поведение под действието на външни сили е разгледана подробно и проучена от английския учен от 19-ти век Томас Йънг. Самото понятие за еластичност обаче е разработено през далечната 1727 г. от швейцарския математик, физик и философ Леонард Ойлер, а първите експерименти, свързани с модула на еластичност, са проведени през 1782 г., тоест 25 години преди работата на Томас Юнг, от венецианския математик и философ Якопо Рикати.
Заслугата на Томас Йънг се крие във факта, че той придаде на теорията за еластичността тънък модерен вид, който впоследствие беше формализиран под формата на прост и след това обобщен закон на Хук.
Физическа природа на еластичността
Всяко тяло се състои от атоми, между които действат силите на привличане и отблъскване. Балансът на тези сили есъстоянието и параметрите на материята при дадени условия. Атомите на твърдо тяло, когато към тях се прилагат незначителни външни сили на опън или компресия, започват да се изместват, създавайки противоположна по посока и равна по големина сила, която има тенденция да върне атомите в първоначалното им състояние.
В процеса на такова изместване на атомите се увеличава енергията на цялата система. Експериментите показват, че при малки деформации енергията е пропорционална на квадрата на тези деформации. Това означава, че силата, като производна по отношение на енергията, се оказва пропорционална на първата степен на деформацията, тоест зависи линейно от нея. Отговаряйки на въпроса какъв е модулът на еластичност, можем да кажем, че това е коефициентът на пропорционалност между силата, действаща върху атома, и деформацията, която тази сила причинява. Измерението на модула на Янг е същото като измерението на налягането (Паскал).
Еластичен лимит
Съгласно дефиницията, модулът на еластичност показва колко напрежение трябва да бъде приложено към твърдо тяло, за да бъде деформацията му 100%. Въпреки това, всички твърди вещества имат граница на еластичност, равна на 1% деформация. Това означава, че ако се приложи подходяща сила и тялото се деформира с количество по-малко от 1%, то след прекратяването на тази сила тялото точно възстановява първоначалната си форма и размери. Ако се приложи твърде голяма сила, при която стойността на деформацията надвишава 1%, след прекратяване на външната сила, тялото вече няма да възстанови първоначалните си размери. В последния случай се говори за наличието на остатъчна деформация, която едоказателство, че границата на еластичност на материала е надвишена.
Модулът на Янг в действие
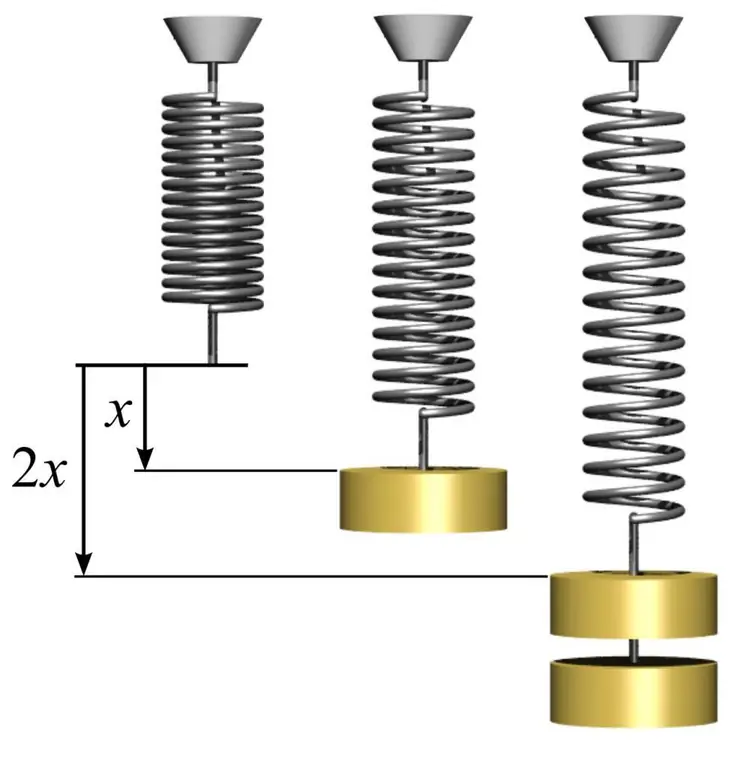
За да определите модула на еластичност, както и да разберете как да го използвате, можете да дадете прост пример с пружина. За да направите това, трябва да вземете метална пружина и да измерите площта на кръга, който образуват нейните намотки. Това се прави с помощта на простата формула S=πr², където n е pi равно на 3,14 и r е радиусът на намотката на пружината.
След това измерете дължината на пружината l0 без товар. Ако окачите някакъв товар с маса m1 на пружина, тогава тя ще увеличи дължината си до определена стойност l1. Модулът на еластичност E може да се изчисли въз основа на познаването на закона на Хук по формулата: E=m1gl0/(S(l 1-l0)), където g е ускорението на свободно падане. В този случай отбелязваме, че размерът на деформация на пружината в еластичната област може значително да надвиши 1%.
Познаването на модула на Янг ви позволява да предвидите размера на деформацията под действието на определено напрежение. В този случай, ако окачим друга маса m2 на пружината, получаваме следната стойност на относителната деформация: d=m2g/ (SE), където d - относителна деформация в еластичната област.
Изотропия и анизотропия
Модулът на еластичност е характеристика на материал, който описва силата на връзката между неговите атоми и молекули, но конкретен материал може да има няколко различни модула на Йънг.
Факт е, че свойствата на всяко твърдо вещество зависят от неговата вътрешна структура. Ако свойствата са еднакви във всички пространствени посоки, тогава говорим за изотропен материал. Такива вещества имат хомогенна структура, така че действието на външна сила в различни посоки върху тях предизвиква една и съща реакция от материала. Всички аморфни материали са изотропни, като гума или стъкло.
Анизотропията е явление, което се характеризира със зависимостта на физичните свойства на твърдо или течност от посоката. Всички метали и сплави на тяхна основа имат една или друга кристална решетка, тоест подредено, а не хаотично подреждане на йонни ядра. За такива материали модулът на еластичност варира в зависимост от оста на действие на външното напрежение. Например, метали с кубична симетрия, като алуминий, мед, сребро, огнеупорни метали и други, имат три различни модула на Янг.
Модул на срязване
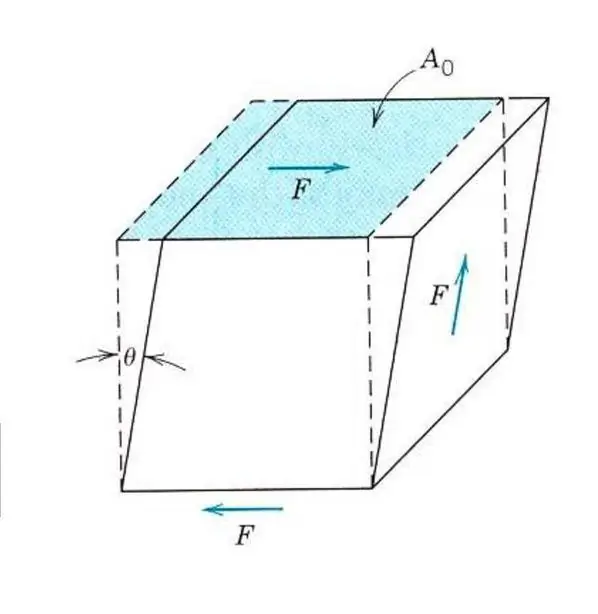
Описание на еластичните свойства дори на изотропен материал не изисква познаване на един модул на Йънг. Тъй като в допълнение към опън и компресия, материалът може да бъде засегнат от напрежения на срязване или напрежения на усукване. В този случай той ще реагира различно на външната сила. За да се опише еластичната деформация на срязване, се въвежда аналог на модула на Young, модула на срязване или модула на еластичност от втория вид.
Всички материали издържат на напрежения на срязване, по-малко от опън или компресия, така че стойността на модула на срязване за тях е 2-3 пъти по-малка от стойността на модула на Йънг. Така за титан, чийто модул на Юнг е равен на 107 GPa, модулът на срязване есамо 40 GPa, за стоманата тези цифри са съответно 210 GPa и 80 GPa.
Модул на еластичност на дървото

Дървото е анизотропен материал, тъй като дървесните влакна са ориентирани в определена посока. Именно по дължината на влакната се измерва модулът на еластичност на дървото, тъй като той е с 1-2 порядъка по-малък през влакната. Познаването на модула на Young за дърво е важно и се взема предвид при проектирането на дървени панелни конструкции.
Стойностите на модула на еластичност на дървесината за някои видове дървета са показани в таблицата по-долу.
| Изглед на дърво | Модул на Янг в GPa |
| Laurel tree | 14 |
| Евкалипт | 18 |
| кедър | 8 |
| смърч | 11 |
| бор | 10 |
| Дъб | 12 |
Трябва да се отбележи, че дадените стойности могат да се различават с до 1 GPa за определено дърво, тъй като неговият модул на Юнг се влияе от плътността на дървесината и условията на отглеждане.

Модулите на срязване за различни дървесни видове са в диапазона от 1-2 GPa, например, за бор е 1,21 GPa, а за дъб 1,38 GPa, тоест дървесината практически не издържа на напрежения на срязване. Този факт трябва да се има предвид при производството на дървени носещи конструкции, които са проектирани да работят само при опън или компресия.
Еластични характеристики на металите
В сравнение с модула на дървесината на Янг, средните стойности на тази стойност за метали и сплави са с порядък по-големи, както е показано в следващата таблица.
| Метал | Модул на Янг в GPa |
| Бронз | 120 |
| Мед | 110 |
| Стомана | 210 |
| Титан | 107 |
| никел | 204 |
Еластични свойства на метали, които имат кубична сингония, се описват с три еластични константи. Такива метали включват мед, никел, алуминий, желязо. Ако металът има шестоъгълна сингония, тогава вече са необходими шест константи, за да опишат неговите еластични характеристики.
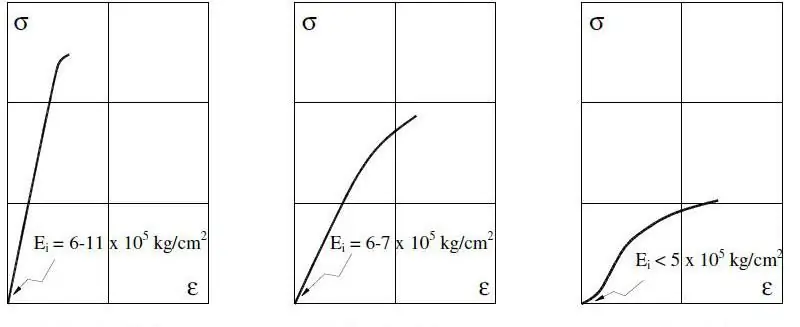
За метални системи модулът на Юнг се измерва в рамките на 0,2% деформация, тъй като големи стойности вече могат да се появят в нееластичния регион.






