Линейната функция е права линия, начертана по повърхността. Може да се раздели на различни видове и модели. По-долу ще разгледаме формулите за получаването му, както и постигането му на съвършенство в равнината. В чертежите можете напълно да проверите това и да разберете как трябва да изглежда.
Линейна функция y=kx + b
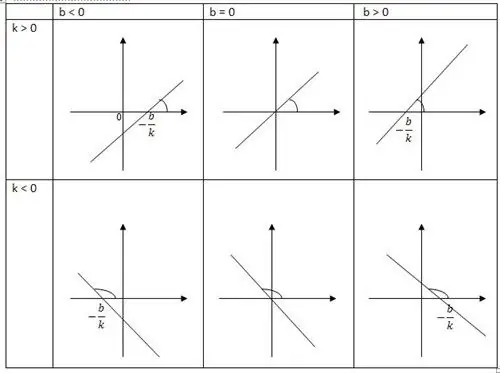
Тази стойност е точна мярка за променлива в един изглед. Инкрементът се отнася до основното свойство на линейна функция, той става пропорционален на увеличения аргумент. С други думи, функцията представлява обобщение на пряката пропорционалност. Правата линия е графика на линейна функция. От тук идва и името му. Една реална променлива докосва друга реална функция.
Свойства
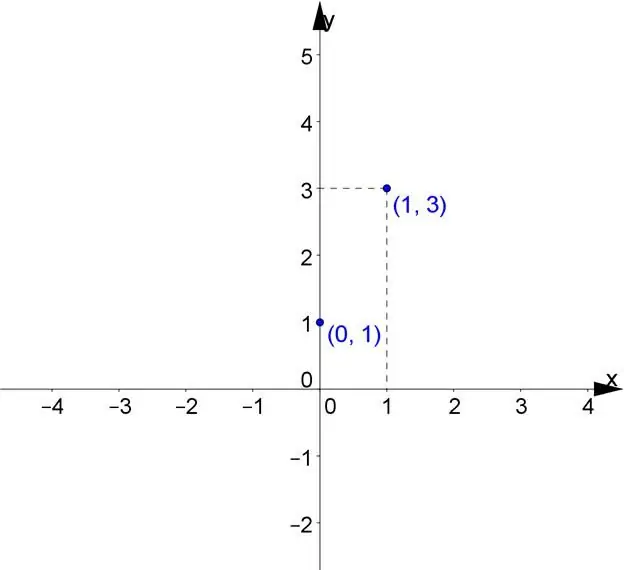
Линейната функция е образуваща на права линия, която има положителна посока на оста x. Един от определящите му коефициенти на наклон е k, той определя тангенса на ъгъла a. Правата линия, образувана в положителната посока на оста x, е k. Другата координата b показвакоординати на точката, както и пресечната точка на правата с оста.
Какво са нелинейни функции?
Функциите, които не са линейни, се наричат нелинейни. Това е математическа връзка между променливите. Нелинейните не могат да се изразят като y=ax + b. Този термин се използва в онези моменти, когато е необходимо да се проучи общият случай. Този процес започва с по-ниските степени. В този случай се вземат предвид квадратичните корекции. Такава функция има непрекъсната кривина.
Разглежданото нелинейно уравнение е произволно. Пример за нелинейна функция е y=x2. Често се използват термините "линейна функция", с усъвършенстване и добавяне на "хомогенна". Може да се приложи към точно линейно картографиране на X, което е векторно пространство. Линейна функция е цялата система като нея.






