Важен раздел от термодинамиката е изследването на трансформациите между различните фази на веществото, тъй като тези процеси протичат на практика и са от основно значение за прогнозиране на поведението на една система при определени условия. Тези трансформации се наричат фазови преходи, на които е посветена статията.
Концепцията за фаза и системен компонент

Преди да се пристъпи към разглеждането на фазовите преходи във физиката, е необходимо да се дефинира концепцията за самата фаза. Както е известно от курса на общата физика, има три състояния на материята: газообразно, твърдо и течно. В специален раздел на науката - в термодинамиката - законите се формулират за фазите на материята, а не за техните агрегатни състояния. Под фаза се разбира определен обем материя, която има хомогенна структура, характеризира се със специфични физични и химични свойства и е отделена от останалата материя чрез граници, които се наричат интерфаза.
По този начин понятието "фаза" носи много по-практически значима информация за свойстватаматерия, отколкото неговото агрегатно състояние. Например, твърдото състояние на метал като желязото може да бъде в следните фази: нискотемпературен магнитно центриран кубик (BCC), нискотемпературен немагнитен bcc, лицево-центриран кубик (fcc) и високо- температура немагнитен Bcc.
В допълнение към концепцията за "фаза", законите на термодинамиката използват и термина "компоненти", което означава броя на химичните елементи, които изграждат определена система. Това означава, че фазата може да бъде монокомпонентна (1 химичен елемент) или многокомпонентна (няколко химични елемента).
теорема на Гибс и равновесие между фазите на системата

За да се разберат фазовите преходи, е необходимо да се знаят условията на равновесие между тях. Тези условия могат да бъдат получени математически чрез решаване на системата от уравнения на Гибс за всяко от тях, като се приеме, че равновесното състояние е достигнато, когато общата енергия на Гибс на системата, изолирана от външно влияние, престане да се променя.
В резултат на решаването на посочената система от уравнения се получават условия за съществуване на равновесие между няколко фази: изолирана система ще престане да се развива само когато наляганията, химическите потенциали на всеки компонент и температурите във всички фази са равни една на друга.
Фазово правило на Гибс за равновесие

Система, състояща се от няколко фази и компоненти, може да бъде в равновесие не самопри определени условия, например при определена температура и налягане. Някои от променливите в теоремата на Гибс за равновесие могат да бъдат променени, като се поддържа както броят на фазите, така и броят на компонентите, които са в това равновесие. Броят на променливите, които могат да се променят, без да се нарушава равновесието в системата, се нарича брой свободи на тази система.
Броят на свободите l на система, състояща се от f фази и k компоненти, се определя еднозначно от правилото за фазите на Гибс. Това правило се записва математически по следния начин: l + f=k + 2. Как да работим с това правило? Много просто. Например, известно е, че системата се състои от f=3 равновесни фази. Какъв е минималният брой компоненти, които може да съдържа една такава система? Можете да отговорите на въпроса, като разсъждавате по следния начин: в случай на равновесие съществуват най-строгите условия, когато се реализира само при определени показатели, тоест промяната в който и да е термодинамичен параметър ще доведе до дисбаланс. Това означава, че броят на свободите l=0. Замествайки известните стойности на l и f, получаваме k=1, тоест система, в която три фази са в равновесие, може да се състои от един компонент. Отличен пример е тройната точка на водата, където ледът, течната вода и парата съществуват в равновесие при определени температури и налягания.
Класификация на фазовите трансформации
Ако започнете да променяте някои термодинамични параметри в система в равновесие, можете да наблюдавате как една фаза ще изчезне и ще се появи друга. Прост пример за този процес е топенето на леда, когато се нагрява.
Като се има предвид, че уравнението на Гибс зависи само от две променливи (налягане и температура) и фазовият преход включва промяна в тези променливи, тогава математически преходът между фазите може да бъде описан чрез диференциране на енергията на Гибс по отношение на нейната променливи. Именно този подход е използван от австрийския физик Пол Еренфест през 1933 г., когато съставя класификация на всички известни термодинамични процеси, които протичат при промяна на фазовото равновесие.
От основите на термодинамиката следва, че първата производна на енергията на Гибс по отношение на температурата е равна на промяната в ентропията на системата. Производната на енергията на Гибс по отношение на налягането е равна на промяната в обема. Ако, когато фазите в системата се променят, ентропията или обемът претърпи прекъсване, тоест те се променят рязко, тогава те говорят за фазов преход от първи ред.
Освен това, вторите производни на енергията на Гибс по отношение на температурата и налягането са съответно топлинният капацитет и коефициентът на обемно разширение. Ако трансформацията между фазите е придружена от прекъсване на стойностите на посочените физически величини, тогава се говори за фазов преход от втори ред.
Примери за трансформации между фази

Има огромен брой различни преходи в природата. В рамките на тази класификация ярки примери за преходи от първи вид са процесите на топене на метали или кондензация на водна пара от въздуха, когато има скок на обема в системата.
Ако говорим за преходи от втори ред, тогава поразителни примери са трансформацията на желязото от магнитно в парамагнитно състояние при температура768 ºC или превръщането на метален проводник в свръхпроводящо състояние при температури, близки до абсолютната нула.
Уравнения, които описват преходи от първия вид
На практика често е необходимо да се знае как се променят температурата, налягането и погълнатата (освободената) енергия в системата, когато в нея настъпят фазови трансформации. За тази цел се използват две важни уравнения. Те се получават въз основа на познаването на основите на термодинамиката:
- Формула на Клапейрон, която установява връзката между налягане и температура по време на трансформации между различните фази.
- Формула на Клаузиус, която свързва погълнатата (освободената) енергия и температурата на системата по време на трансформацията.
Използването на двете уравнения е не само за получаване на количествени зависимости на физическите величини, но също така и за определяне на знака на наклона на равновесните криви върху фазовите диаграми.
Уравнение за описване на преходи от втория вид

Фазовите преходи от 1-ви и 2-ри вид се описват с различни уравнения, тъй като прилагането на уравненията на Клаузиус и Клаузиус за преходи от втори ред води до математическа несигурност.
За да се опише последното, се използват уравненията на Еренфест, които установяват връзка между промените в налягането и температурата чрез познаване на промените в топлинния капацитет и коефициента на обемно разширение по време на процеса на трансформация. Уравненията на Еренфест се използват за описване на преходи проводник-свръхпроводник при отсъствие на магнитно поле.
Важностфазови диаграми
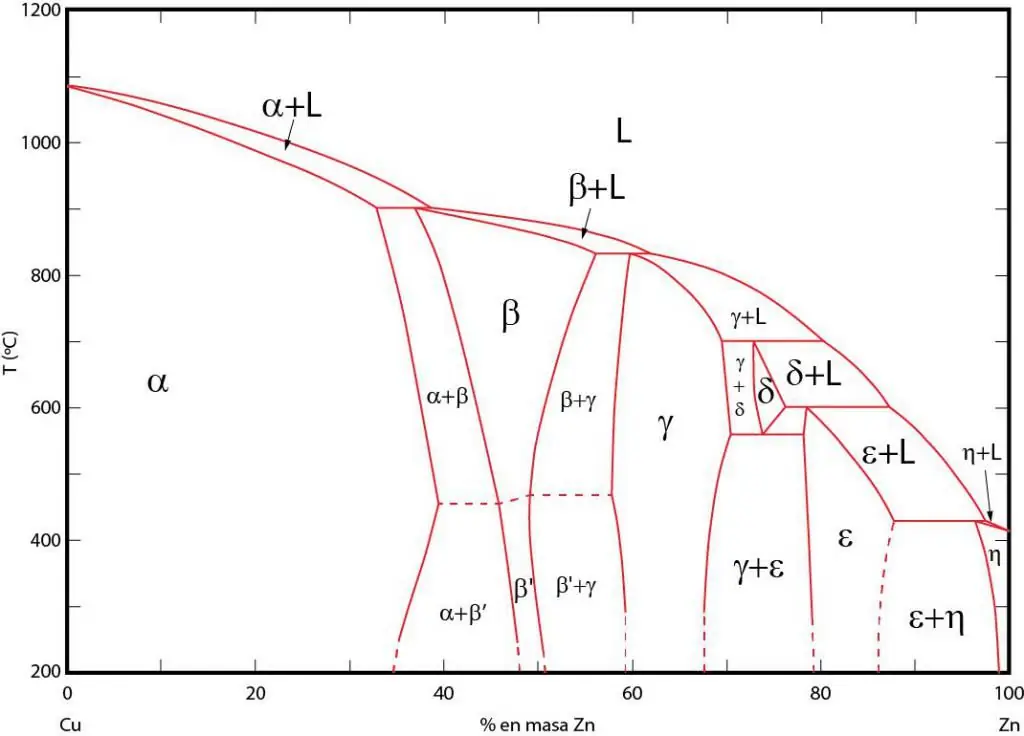
Фазовите диаграми са графично представяне на области, в които съответните фази съществуват в равновесие. Тези области са разделени от равновесни линии между фазите. Често се използват фазови диаграми P-T (налягане-температура), T-V (температура-обем) и P-V (налягане-обем).
Важността на фазовите диаграми се крие във факта, че те ви позволяват да предскажете в каква фаза ще бъде системата, когато външните условия се променят съответно. Тази информация се използва при топлинната обработка на различни материали, за да се получи структура с желаните свойства.






